高级排序算法

这一节介绍几种高级排序算法，他们都采用了算法中分治思想。

• 希尔排序
• 快速排序
• 归并排序
• 堆排序

希尔排序

它会首先比较较远的元素而非相邻的元素。让元素尽快回到正确的位置。通过定义一个间隔序列来表示在排序过程中进行比较的元素间。公开的间隔序列是 701，301，132，57，23，10，4，1.(质数)。

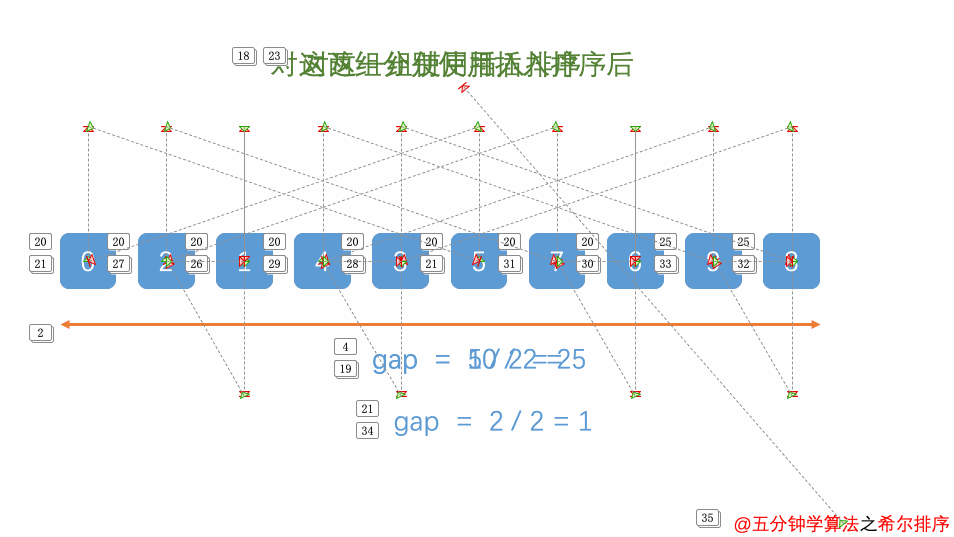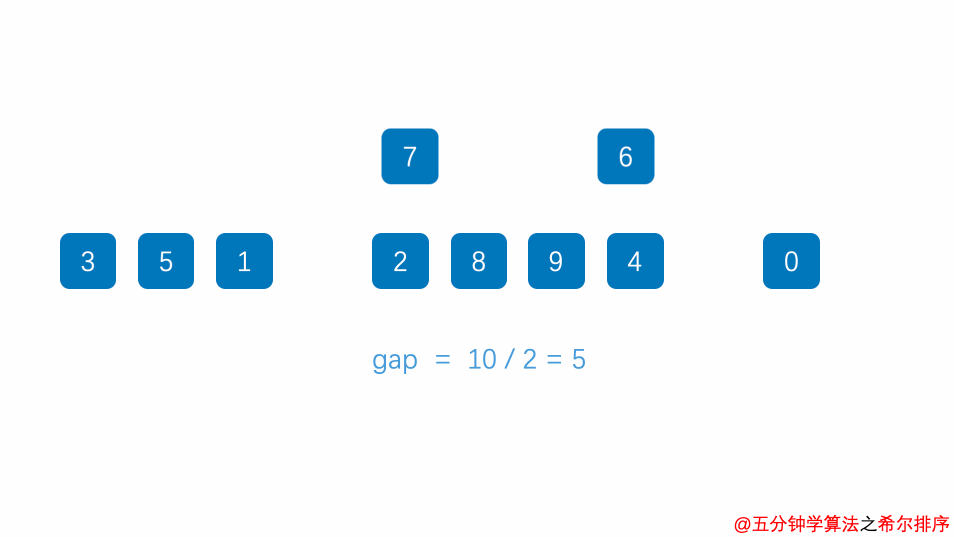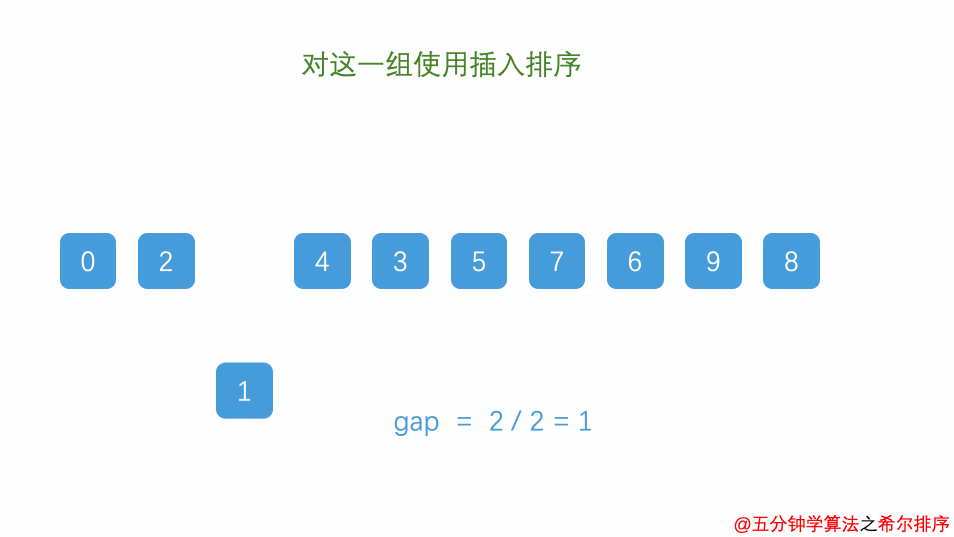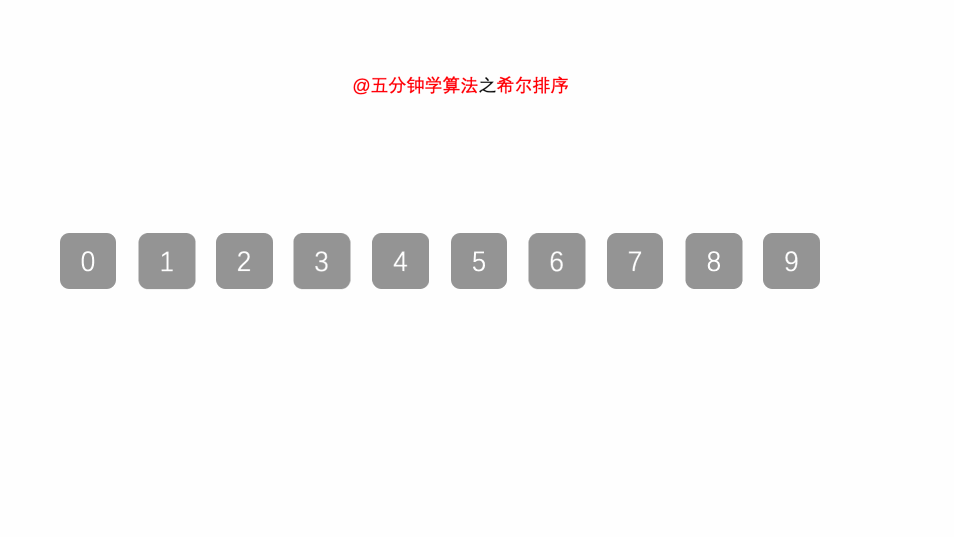
function shellSort(array) {
  // 定义间隔序列，这里写死了，可以动态定义
  const gaps = [5, 3, 1];
  for (let index = 0; index < gaps.length; index++) {
    const gap = gaps[index];

    for (let outer = gap; outer < array.length; outer++) {
      // 检查的数字
      const temp = array[outer];
      for (
        let inner = outer - gap;
        // 如果比之前的 gap 小，就交换一下，直到交换到第一个 gap 处
        inner >= 0 && array[inner] > temp;
        inner -= gap
      ) {
        swap(array, inner, inner + gap);
      }
    }
  }
  return array;
}

function swap(array, index1, index2) {
  var temp = array[index1];
  array[index1] = array[index2];
  array[index2] = temp;
}

快速排序

在列表中选择一个元素作为基准值，排序围绕这个基准值进行，将列表中小于基准值的放入数组底部大于放顶部。

function qSort(list) {
  if (list.length == 0) {
    return [];
  }
  var pivot = list[0];
  var lesser = [];
  var greater = [];
  for (var i = 1; i < list.length; i++) {
    if (list[i] < pivot) {
      lesser.push(list[i]);
    } else {
      greater.push(list[i]);
    }
  }
  return qSort(lesser).concat(pivot, qSort(greater));
}
var myArray = [2, 3, 1, 9, 6, 4, 7, 8, 5];
var arr = qSort(myArray);
console.log(arr);

归并排序

把一系列排好序的子序列合并成一个大的完整有序序列。

// 归并排序算法
function mergeSort(array) {
  // 避免污染传入的数组
  const temp = [...array];
  splitArray(temp, 0, array.length - 1);
  return temp;
}

// 将大数组拆分成两个小数组
function splitArray(array, start, end) {
  if (start < end) {
    const mid = Math.floor((start + end) / 2);
    splitArray(array, 0, mid);
    splitArray(array, mid + 1, end);
    mergeArray(array, start, mid, end);
  }
}

// 合并两个排序好的数组
function mergeArray(array, start, mid, end) {
  var i = start;
  var j = mid + 1;
  var k = 0;
  var temp = [];
  while (i <= mid && j <= end) {
    if (array[i] <= array[j]) {
      temp[k] = array[i];
      i++;
    } else {
      temp[k] = array[j];
      j++;
    }
    k++;
  }

  while (i <= mid) {
    temp[k] = array[i];
    i++;
    k++;
  }

  while (j <= end) {
    temp[k] = array[j];
    j++;
    k++;
  }

  for (let index = 0; index < k; index++) {
    array[index + start] = temp[index];
  }
}
var arr = [2, 3, 7, 9, 8, 5, 4, 6, 1];
console.log("原始数组：", arr);
const result = mergeSort(arr);
console.log("排列后数组：", result);

堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为 O(nlogn)，它也是不稳定排序。

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

堆排序适合于树形结构的数据结构。分为 2 个步骤排序：

1、构建大顶堆。

2、取出大顶堆顶端的值，为最大的值。

3、重新构建大顶堆，继续走第二步，直到堆中的数据为空。